Latent Dirichlet Allocation

From https://en.wikipedia.org/wiki/Latent_Dirichlet_allocation:

In natural language processing, latent Dirichlet allocation (LDA) is a generative statistical model that allows sets of observations to be explained by unobserved groups that explain why some parts of the data are similar. For example, if observations are words collected into documents, it posits that each document is a mixture of a small number of topics and that each word's creation is attributable to one of the document's topics. LDA is an example of a topic model...

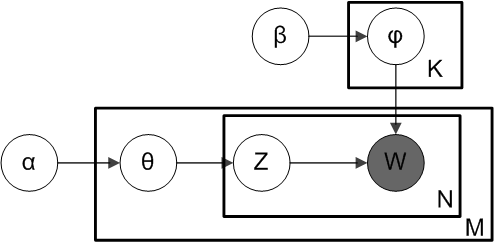
The generative process is as follows. Documents are represented as random mixtures over latent topics, where each topic is characterized by a distribution over words. LDA assumes the following generative process for a corpus \(D\) consisting of \(M\) documents each of length \(N_i\):

1. Choose \( \theta_i \, \sim \, \mathrm{Dir}(\alpha) \), where \( i \in \{ 1,\dots,M \} \) and \( \mathrm{Dir}(\alpha) \) is the Dirichlet distribution for parameter \(\alpha\)
2. Choose \( \varphi_k \, \sim \, \mathrm{Dir}(\beta) \), where \( k \in \{ 1,\dots,K \} \)
3. For each of the word positions \(i, j\), where \( j \in \{ 1,\dots,N_i \} \), and \( i \in \{ 1,\dots,M \} \)
   1. Choose a topic \(z_{i,j} \,\sim\, \mathrm{Categorical}(\theta_i). \)
   2. Choose a word \(w_{i,j} \,\sim\, \mathrm{Categorical}( \varphi_{z_{i,j}}) \).

This is a smoothed LDA model to be precise. The subscript is often dropped, as in the plate diagrams shown here.

The aim is to compute the word probabilities of each topic, the topic of each word, and the particular topic mixture of each document. This can be done with Bayesian inference: the documents in the dataset represent the observations (evidence) and we want to compute the posterior distribution of the above quantities.

Suppose we have two topics, indicated with integers 1 and 2, and 10 words, indicated with integers \(1,\ldots,10\).

Predicate word(Doc,Position,Word) indicates that document Doc in position Position (from 1 to the number of words of the document) has word Word

Predicate topic(Doc,Position,Topic) indicates that document Doc associates topic Topic to the word in position Position

We can use the model generatively and sample values for word in position 1 of document 1:

Also generatively, we can sample values for couples (word,topic) in position 1 of document 1:

We can use the model to classify the words in topics: assigning words to topics. Here we use conditional inference with Metropolis-Hastings.

A priori both topics are about equally probable for word 1 of document 1.

After observing that words 1 and 2 of document 1 are equal, one of the topics gets more probable.

You can also see this if you look at the distribution of the probability of topic 1 before and after observing that words 1 and 2 of document 1 are equal: the observation makes the distribution less uniform.

Code

You can change the number of words in vocabulary and the number of topics by modifying the facts for n_words/1 and n_topics/1.

The distributions for both \(\theta_m\) and \(\varphi_k\) are symmetric Dirichlet distributions with scalar concentration parameter \(\eta\) set using a fact for the predicate eta/1. In other words \(\alpha=\beta=[\eta,\ldots,\eta]\).

References

[1] Blei, David M., Andrew Y. Ng, and Michael I. Jordan. "Latent dirichlet allocation." Journal of machine Learning research 3.Jan (2003): 993-1022.

[2] https://en.wikipedia.org/wiki/Latent_Dirichlet_allocation